某市为了解八年级学生视力健康状况,在全市随机抽查了400名八年级学生2021年初的视力数据,并调取该批学生2020年初的视力数据,制成如图统计图(不完整)

青少年视力健康标准
类别 |
视力 |
健康状况 |
|
视力 |
视力正常 |
|
4.9 |
轻度视力不良 |
|
视力 |
中度视力不良 |
|
视力 |
重度视力不良 |
根据以上信息,请解答:
(1)分别求出被抽查的400名学生2021年初轻度视力不良(类别 的扇形圆心角度数和2020年初视力正常(类别 的人数.
(2)若2021年初该市有八年级学生2万人,请估计这些学生2021年初视力正常的人数比2020年初增加了多少人?
(3)国家卫健委要求,全国初中生视力不良率控制在 以内.请估计该市八年级学生2021年初视力不良率是否符合要求?并说明理由.
计算:(x+y)2-y(2x+y)
(2)先计算,再把计算所得的多项式分解因式:(12a3-12a2+3a)÷3a.
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.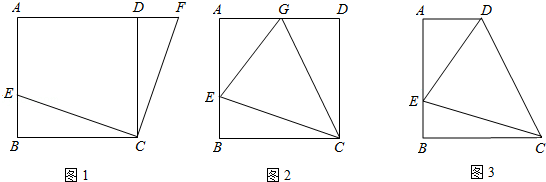
有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克?
已知:Rt△ABC中,∠C=90°,∠CAB的平分线与外角∠CBE的平分线相交于点D.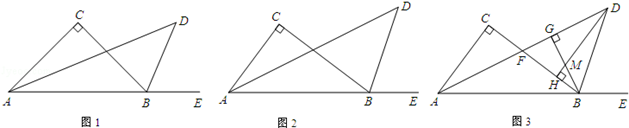
(1)如图1,若CA=CB,则∠D= 度;
(2)如图2,若CA≠CB,求∠D的度数;
(3)如图3,在(2)的条件下,AD与BC相交于点F,过B作BG⊥DF,过D作DH⊥BF,垂足分别为G,H,BG,DH相交于点M.若FG=2,DG=4,求BH的长.
如图,在▱ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作平行四边形AGDB交CB的延长线于点G.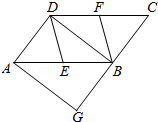
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.