小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形 绕点 顺时针旋转 ，得到矩形 ，连结 ．
探究 如图1，当 时，点 恰好在 延长线上．若 ，求 的长．
探究 如图2，连结 ，过点 作 交 于点 ．线段 与 相等吗？请说明理由．
探究 在探究2的条件下，射线 分别交 ， 于点 ， （如图 ，发现线段 ， ， 存在一定的数量关系，请写出这个关系式，并加以证明．
某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件；
（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？
（2）每件衬衫降价多少元时，商场平均每天赢利最多？
如图：E、F分别是正方形ABCD的边CD、DA上一点，且CE+AF=EF，请你用旋转的方法求∠EBF的大小．
要对一块长60米，宽40米的矩形荒地ABCD进行绿化和硬化、设计方案如图所示，矩形P、Q为两块绿地，其余为硬化路面，P、Q两块绿地周围的硬化路面宽都相等，并使两块绿地面积的和为矩形ABCD面积的
，求P、Q两块绿地周围的硬化路面的宽．
如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（0，1），B（﹣1，1），C（﹣1，3）．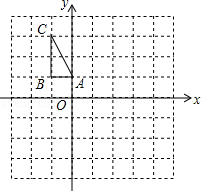
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2；
（3）△OB2P为等腰三角形，且P在x轴上，请直接写出所有符合条件的P点坐标．
选择适当的方法解一元二次方程：
（1）x2+2x﹣15=0
（2）4x﹣6=（3﹣2x）x．