已知函数f(x)=2lnx+1.
(1)若f(x)≤2x+c,求c的取值范围;
(2)设a>0时,讨论函数g(x)= 的单调性.
(本小题满分12分)
设函数
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知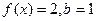 ,△ABC的面积为
,△ABC的面积为 的值。
的值。
设函数 .
.
(Ⅰ)当 曲线
曲线 处的切线斜率;
处的切线斜率;
(Ⅱ)求函数的单调区间与极值
(Ⅲ)已知方程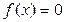 有三个互不相同的实根0,
有三个互不相同的实根0, ,且
,且 .若对任意的
.若对任意的 ,
, 恒成立,求m的取值范围
恒成立,求m的取值范围
等比数列{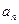 }的前n项和为
}的前n项和为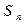 ,已知对任意的
,已知对任意的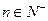 ,点
,点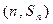 均在函数
均在函数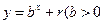 且
且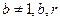 均为常数)的图像上.
均为常数)的图像上.
(Ⅰ)求r的值
(Ⅱ)当b=2时,记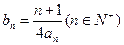 ,数列
,数列 的前n项和
的前n项和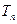 ,求证:
,求证: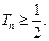
平面直角坐标系中,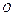 为坐标原点,给定两点A(1,0)、B(0,-2),点C满足
为坐标原点,给定两点A(1,0)、B(0,-2),点C满足 其中
其中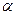 、
、 且
且 .
.
(Ⅰ)求点C的轨迹方程;
(Ⅱ)设点C的轨迹与双曲线 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: 为定值.
为定值.
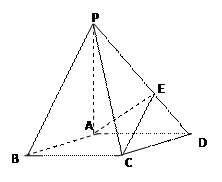 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD= ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角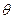 的大小.
的大小.
|