已知 是无穷数列.给出两个性质:
①对于 中任意两项 ,在 中都存在一项 ,使 ;
②对于 中任意项 ,在 中都存在两项 .使得 .
(Ⅰ)若 ,判断数列 是否满足性质①,说明理由;
(Ⅱ)若 ,判断数列 是否同时满足性质①和性质②,说明理由;
(Ⅲ)若 是递增数列,且同时满足性质①和性质②,证明: 为等比数列.
(本题14分)A、B是直线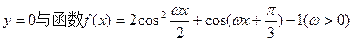 图像的两个相邻交点,且
图像的两个相邻交点,且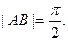
(I)求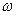 的值;
的值;
(II)在锐角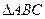 中,a,b,c分别是角A,B,C的对边,若
中,a,b,c分别是角A,B,C的对边,若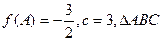 的面积为
的面积为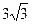 ,求a的值.
,求a的值.
(本小题满分10分)选修4-5:不等式选讲
关于 的不等式
的不等式
(Ⅰ)当 时,解不等式;
时,解不等式;
(Ⅱ)设函数 ,当
,当 为何值时,
为何值时, 恒成立?
恒成立?
(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系 内,点
内,点 在曲线C:
在曲线C: 为参数,
为参数, )上运动.以
)上运动.以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)写出曲线C的标准方程和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求 面积的
面积的
最大值.
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若 ,试求
,试求 的大小.
的大小.
(本小题满分12分)
若函数f(x)= 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(Ⅰ)求正实数a的取值范围.
(Ⅱ)若a=1,求征:


 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )