设集合S，T，S⊆N，T⊆N，S，T中至少有两个元素，且S，-优题课

题文

设集合 S， T， S $\subseteq$ N ^*， T $\subseteq$ N ^*， S， T中至少有两个元素，且 S， T满足：

①对于任意 x， y $\in$ S，若 x≠ y，都有 xy $\in$ T

②对于任意 x， y $\in$ T，若 x< y，则 $\frac{y}{x} \in$ S；

下列命题正确的是（）

科目数学题型选择题难度中等

相关试题

如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和，过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB∶A′B′＝
（A）2∶1（B）3∶1（C）3∶2（D）4∶3

过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为
（A） (B) (C) (D)

给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线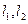与同一平面所成的角相等,则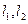互相平行.
④若直线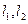是异面直线,则与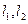都相交的两条直线是异面直线.
其中假命题的个数是

两相同的正四棱锥组成如图1所示的几何体，可放棱长为1的正方体内，使正四棱锥的底面ABCD与正方体的某一个平面平行，且各顶点均在正方体的面上，则这样的几何体体积的可能值有

过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°则该截面的面积是