如图,已知椭圆 ,抛物线 ,点 A是椭圆 与抛物线 的交点,过点 A的直线 l交椭圆 于点 B,交抛物线 于 M( B, M不同于 A).

(Ⅰ)若 ,求抛物线 的焦点坐标;
(Ⅱ)若存在不过原点的直线 l使 M为线段 AB的中点,求 p的最大值.
设椭圆 :
: 的离心率为
的离心率为 ,点
,点 (
(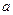 ,0),
,0), (0,
(0, ),原点
),原点 到直线
到直线 的距离为
的距离为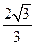 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设点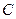 为(
为(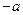 ,0),点
,0),点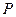 在椭圆
在椭圆 上(与
上(与 、
、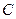 均不重合),点
均不重合),点 在直线
在直线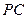 上,若直线
上,若直线 的方程为
的方程为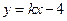 ,且
,且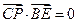 ,试求直线
,试求直线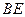 的方程.
的方程.
(本小题满分14分)如果对于函数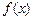 的定义域内任意的
的定义域内任意的 ,都有
,都有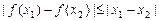 成立,那么就称函数
成立,那么就称函数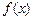 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数 ,
,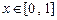 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数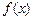 是闭区间
是闭区间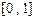 上的“平缓函数”,且
上的“平缓函数”,且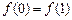 .证明:对于任意的
.证明:对于任意的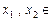
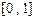 ,都有
,都有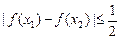 成立.(3)设
成立.(3)设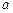 、
、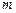 为实常数,
为实常数,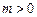 .若
.若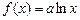 是区间
是区间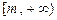 上的“平缓函数”,试估计
上的“平缓函数”,试估计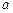 的取值范围(用
的取值范围(用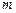 表示,不必证明).
表示,不必证明).
(本小题满分14分)已知数列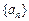 的前
的前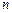 项和
项和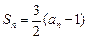 ,
,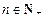 .
.
(1)求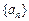 的通项公式;(2)设
的通项公式;(2)设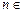 N+,集合
N+,集合 ,
,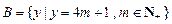 .现在集合
.现在集合 中随机取一个元素
中随机取一个元素 ,记
,记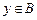 的概率为
的概率为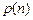 ,求
,求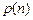 的表达式.
的表达式.
(本小题满分14分)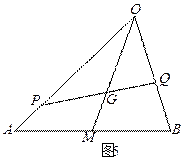 如图5,
如图5,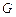 是△
是△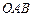 的重心,
的重心,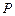 、
、 分别是边
分别是边 、
、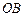 上的动点,且
上的动点,且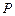 、
、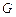 、
、 三点共线.(1)设
三点共线.(1)设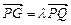 ,将
,将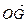 用
用 、
、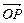 、
、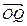 表示;
表示;
(2)设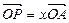 ,
,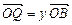 ,证明:
,证明: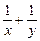 是定值;
是定值;
(3)记△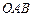 与△
与△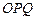 的面积分别为
的面积分别为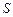 、
、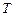 .求
.求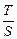 的取值范围.
的取值范围.
(本小题满分14分)已知函数 满足
满足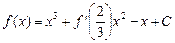 (其中
(其中 为
为 在点
在点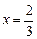 处的导数,
处的导数, 为常数).(1)求函数
为常数).(1)求函数 的单调区间;(2)若方程
的单调区间;(2)若方程 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数 ;(3)在(2)的条件下,若
;(3)在(2)的条件下,若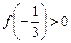 ,求函数
,求函数 的图象与
的图象与 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.