日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为 O),地球上一点 A的纬度是指 OA与地球赤道所在平面所成角,点 A处的水平面是指过点 A且与 OA垂直的平面.在点 A处放置一个日晷,若晷面与赤道所在平面平行,点 A处的纬度为北纬40°,则晷针与点 A处的水平面所成角为( )

| A. |
20° |
B. |
40° |
| C. |
50° |
D. |
90° |
已知数列 中,
中, ,则下列关于
,则下列关于 的说法正确的是
的说法正确的是
| A.一定为等差数列 |
| B.一定为等比数列 |
| C.可能为等差数列,但不会为等比数列 |
| D.可能为等比数列,但不会为等差数列 |
从6人中选4人分别到北京、哈尔滨、广州、成都四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且在这6人中甲、乙不去哈尔滨游览,则不同的选择方案共有
| A.300种 | B.240种 | C.144种 | D.96种 |
设 是两个非零向量,则下列结论不正确的是
是两个非零向量,则下列结论不正确的是
A.若存在一个实数 满足 满足 ,则 ,则 与 与 共线 共线 |
B.若 ,则 ,则 |
C. |
D.若 与 与 为两个方向相同的向量,则 为两个方向相同的向量,则 |
为了得到函数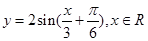 的图像,只需把函数
的图像,只需把函数 的图像上所有的点
的图像上所有的点
A.向左平移 个单位长度,再把所得各点的横坐标缩短为原来的 个单位长度,再把所得各点的横坐标缩短为原来的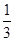 倍(纵坐标不变) 倍(纵坐标不变) |
B.向右平移 个单位长度,再把所得各点的横坐标缩短为原来的 个单位长度,再把所得各点的横坐标缩短为原来的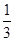 倍(纵坐标不变) 倍(纵坐标不变) |
C.向左平移 个单位长度,再把所得各点的横坐标伸长为原来的 个单位长度,再把所得各点的横坐标伸长为原来的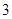 倍(纵坐标不变) 倍(纵坐标不变) |
D.向右平移 个单位长度,再把所得各点的横坐标伸长为原来的 个单位长度,再把所得各点的横坐标伸长为原来的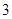 倍(纵坐标不变) 倍(纵坐标不变) |
“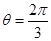 ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |