已知椭圆C: 的离心率为 ,且过点A(2,1).
(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
(本小题共13分)已知函数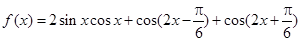 ,
,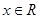 .
.
(Ⅰ)求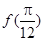 的值;
的值;
(Ⅱ)求函数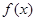 在区间
在区间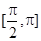 上的最大值和最小值,及相应的x的值.
上的最大值和最小值,及相应的x的值.
(本小题满分13分)已知平面向量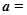
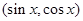 ,
,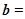
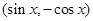 ,
,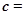
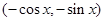 ,
,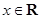 ,函数
,函数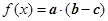 .
.
(Ⅰ)求函数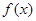 的单调递减区间;
的单调递减区间;
(Ⅱ)若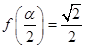 ,求
,求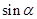 的值.
的值.
(本小题满分13分)某幼儿园有教师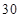 人,对他们进行年龄状况和受教育程度的调查,其结果如下:
人,对他们进行年龄状况和受教育程度的调查,其结果如下:
| 本科 |
研究生 |
合计 |
|
| 35岁以下 |
5 |
2 |
7 |
| 35~50岁(含35岁和50岁) |
17 |
3 |
20 |
| 50岁以上 |
2 |
1 |
3 |
(Ⅰ)从该幼儿园教师中随机抽取一人,求具有研究生学历的概率;
(Ⅱ)从幼儿园所有具有研究生学历的教师中随机抽取2人,求有35岁以下的研究生或50岁以上的研究生的概率.
(本小题满分14分)已知离心率为 的椭圆
的椭圆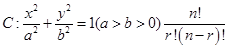 与直线
与直线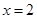 相交于
相交于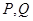 两点(点
两点(点 在
在 轴上方),且
轴上方),且 .点
.点 是椭圆上位于直线
是椭圆上位于直线 两侧的两个动点,且
两侧的两个动点,且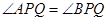 .
.
(Ⅰ)求椭圆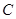 的标准方程;
的标准方程;
(Ⅱ)求四边形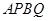 面积的取值范围.
面积的取值范围.
(本小题满分13分)已知函数 .
.
(Ⅰ)若x=1是 的极值点,求a的值:
的极值点,求a的值:
(Ⅱ)当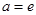 时,求证:
时,求证: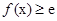 .
.