为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了 天空气中的 和 浓度(单位: ),得下表:
|
|
|
|
|
32 |
18 |
4 |
|
6 |
8 |
12 |
|
3 |
7 |
10 |
(1)估计事件"该市一天空气中 浓度不超过 ,且 浓度不超过 "的概率;
(2)根据所给数据,完成下面的 列联表:
|
|
|
|
||
|
(3)根据(2)中的列联表,判断是否有 的把握认为该市一天空气中 浓度与 浓度有关?
附: ,
|
0.050 |
0.010 |
0.001 |
|
3.841 |
6.635 |
10.828 |
如图,正方体ABCD—A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.
已知定义在R上的函数f(x)=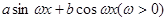 的周期为
的周期为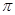 ,且对一切x
,且对一切x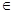 R,都有f(x)
R,都有f(x)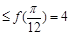 ;
;
(1)求函数f(x)的表达式;
(2)若g(x)=f(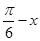 ),求函数g(x)的单调增区间;
),求函数g(x)的单调增区间;
已知函数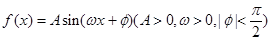 在一个周期内的图像下图所示。
在一个周期内的图像下图所示。
(1)求函数的解析式;
(2)设 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
正项数列 中,前n项和为
中,前n项和为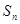 ,且
,且 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设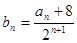 ,
, ,证明
,证明 .
.
设数列{ }是等差数列,
}是等差数列,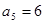 ,
, 时,若自然数
时,若自然数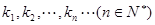 满足
满足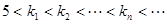 ,使得
,使得 成等比数列,(1)求数列{
成等比数列,(1)求数列{ }的通项公式;(2)求数列
}的通项公式;(2)求数列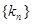 的通项公式及其前n项的和
的通项公式及其前n项的和