如图,四棱锥 P- ABCD的底面为正方形, PD⊥底面 ABCD.设平面 PAD与平面 PBC的交线为 l.

(1)证明: l⊥平面 PDC;
(2)已知 PD= AD=1, Q为 l上的点,求 PB与平面 QCD所成角的正弦值的最大值.
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=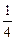 x2的焦点,离心率等于
x2的焦点,离心率等于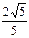 .
.求椭圆C的方程;
过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若
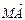 =λ1
=λ1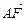 ,
,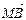 =λ2
=λ2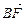 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
已知数列{an}中,an=2-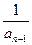 ( n≥2,n∈N+)
( n≥2,n∈N+)若a1=
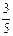 ,数列{bn}满足bn=
,数列{bn}满足bn=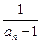 ( n∈N+),求证数列{bn}是等差数列;
( n∈N+),求证数列{bn}是等差数列;若a1=
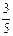 ,求数列{an}中的最大项与最小项,并说明理由.
,求数列{an}中的最大项与最小项,并说明理由.若1<a1<2, 试证:1<an+1< an<2
 如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.求此正三棱柱的侧棱长;
求二面角A-BD-C的大小;
求点C到平面ABD的距离.
某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提高通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响. 求:分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
试用统计知识分析比较两考生的实验操作能力.
设函数f (x)="2cosx" (cosx+ sinx)-1,x∈R
sinx)-1,x∈R求f (x)的最小正周期T;
求f (x)的单调递增区间.