如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是PB的中点,点F是EB的中点.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: 平面
平面 .
.
已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,求tanC的值.
在△ABC中,a、b、c分别表示三个内角A、B、C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断三角形的形状.
已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.
(1)求证:(a-b)⊥c;
(2)若|ka+b+c|>1 (k∈R),求k的取值范围.
已知点G为△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且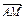 =x
=x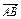 ,
,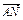 =y
=y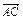 ,求
,求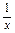 +
+ 的值.
的值.
在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB= OB.DC与OA交于E,设
OB.DC与OA交于E,设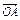 =a,
=a, =b,用a,b表示向量
=b,用a,b表示向量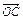 ,
,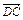 .
.