设函数 , 曲线 在点 处的切线方程为 ,
(1)求 的值;
(2)求 的单调区间;
在平面直角坐标系 中,抛物线
中,抛物线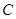 的顶点在原点,经过点
的顶点在原点,经过点 ,其焦点
,其焦点 在
在 轴上,
轴上,
(1)求抛物线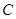 的标准方程;
的标准方程;
(2)求过点 ,且与直线
,且与直线 垂直的直线方程;
垂直的直线方程;
(3)设过点 的直线交抛物线
的直线交抛物线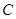 于
于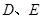 两点,
两点,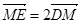 ,记
,记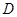 和
和 两点间的距离为
两点间的距离为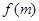 ,求
,求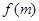 关于
关于 的表达式.
的表达式.
如图,正四棱柱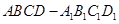 中,
中,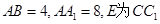 的中点,
的中点,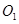 为下底面正方形的中心,
为下底面正方形的中心,
(1)求证: ;
;
(2)求异面直线 所成角的余弦值;
所成角的余弦值;
(3)求二面角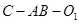 的余弦值.
的余弦值.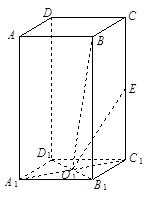
已知圆 :
: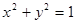 ,点
,点 在直线
在直线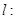
 上,过点
上,过点 作圆
作圆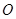 的两条切线,
的两条切线,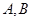 为两切点,
为两切点,
(1)求切线长 的最小值,并求此时点
的最小值,并求此时点 的坐标;
的坐标;
(2)点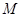 为直线
为直线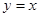 与直线
与直线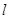 的交点,若在平面内存在定点
的交点,若在平面内存在定点 (不同于点
(不同于点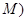 ,满足:对于圆
,满足:对于圆 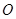 上任意一点
上任意一点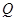 ,都有
,都有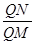 为一常数,求所有满足条件的点
为一常数,求所有满足条件的点 的坐标;
的坐标;
(3)求 的最小值.
的最小值.
如图,已知椭圆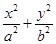 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为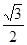 .
.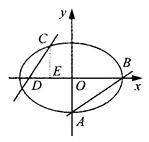
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.
问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
如图,已知四棱锥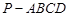 中,底面
中,底面 是直角梯形,
是直角梯形,
 是线段
是线段 上不同于
上不同于 的任意一点,且
的任意一点,且

(1)求证: ;
;
(2)求证: ;
;
(3)求三棱锥 的体积。
的体积。