图1是由矩形 和菱形 组成的一个平面图形,其中 , ,将其沿 折起使得 与 重合,连结 ,如图2.
(1)证明图2中的 四点共面,且平面 平面 ;
(2)求图2中的四边形 的面积.

设函数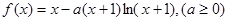 。
。
(1)如果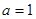 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(2)若函数 在区间
在区间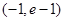 上单调递增,求实数
上单调递增,求实数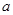 的取值范围;
的取值范围;
(3)证明:当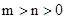 时,
时,
已知函数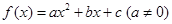 满足
满足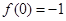 ,对任意
,对任意 都有
都有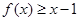 ,且
,且 .
.
(1)求函数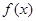 的解析式;
的解析式;
(2)是否存在实数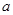 ,使函数
,使函数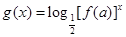 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数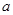 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
某厂生产某种产品的年固定成本为 万元,每生产
万元,每生产 千件,需另投入成本为
千件,需另投入成本为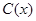 .当年产量不足
.当年产量不足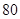 千件时,
千件时,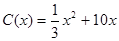 (万元).当年产量不小于
(万元).当年产量不小于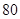 千件时,
千件时, (万元).每件商品售价为
(万元).每件商品售价为 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
已知 中,内角
中,内角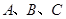 的对边的边长为
的对边的边长为 ,且
,且
(1)求角 的大小;
的大小;
(2)若 ,
,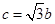 ,求出
,求出 的面积
的面积
已知函数
(1)若 求
求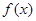 的值;
的值;
(2)求函数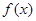 最小正周期及单调递减区间.
最小正周期及单调递减区间.