设函数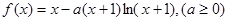 。
。
(1)如果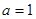 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(2)若函数 在区间
在区间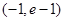 上单调递增,求实数
上单调递增,求实数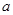 的取值范围;
的取值范围;
(3)证明:当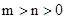 时,
时,
已知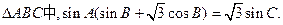
(Ⅰ)求角A的大小 ;
;
(Ⅱ)若BC=3,求 周长的取值范围。
周长的取值范围。
设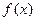 是定义在[-1,1]上的奇函数,且对任意
是定义在[-1,1]上的奇函数,且对任意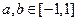 ,当
,当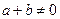 时,都有
时,都有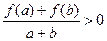 .
.
(1)若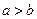 ,试比较
,试比较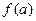 与
与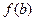 的大小;
的大小;
(2)解不等式
(3)如果 和
和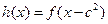 这两个函数的定义域的交集为空集,求
这两个函数的定义域的交集为空集,求 的取值范围.
的取值范围.
在数列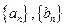 中,
中, 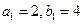 ,且
,且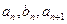 成等差数列,
成等差数列, 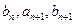 成等比数列
成等比数列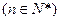 .
.
(1)求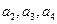 及
及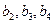 ,由此猜测
,由此猜测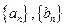 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明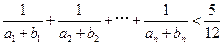 .
.
请先阅读:在等式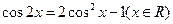 的两边对x求导
的两边对x求导
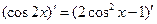 .由求导法则得
.由求导法则得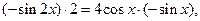 化简后得等式
化简后得等式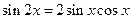 利用上述想法(或者其他方法),试由等式
利用上述想法(或者其他方法),试由等式
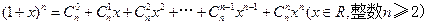 ,
,
证明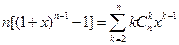

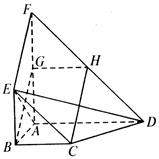
如图,平面ABEF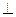 ABCD,四边形ABEF与ABCD都是直角梯形,
ABCD,四边形ABEF与ABCD都是直角梯形, 
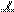
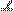
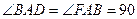 °,BC
°,BC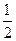 AD,BE
AD,BE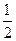 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.

(1)证明四边形BCHG是平行四边行.
(2)C、D、E、F四点是否共面?为什么?
(3)设AB=BE,证明平面ADE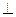 平面CDE.
平面CDE.