如图,在极坐标系 中, , , , ,弧 , , 所在圆的圆心分别是 , , ,曲线 是弧 ,曲线 是弧 ,曲线 是弧 .

(1)分别写出 , , 的极坐标方程;
(2)曲线 由 , , 构成,若点 在 上,且 ,求 的极坐标.
已知函数f(x)=x2-2acos kπ·ln x(k∈N*,a∈R,且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2 04,关于x的方程f(x)=2ax有唯一解,求a的值.
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)=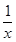 在(0,1]上解的个数.
在(0,1]上解的个数.
已知函数f(x)=ln x+2x,g(x)=a(x2+x).
(1)若a= ,求F(x)=f(x)-g(x)的单调区间;
,求F(x)=f(x)-g(x)的单调区间;
(2)若f(x)≤g(x)恒成立,求实数a的取值范围.
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)的单调区间.
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.