如图,在三棱锥 中, , , 为 的中点.
(1)证明: 平面 ;
(2)若点 在棱 上,且 ,求点 到平面 的距离.

已知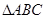 内角
内角 所对的边分别是
所对的边分别是 ,且
,且 .
.
(1)若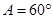 ,求
,求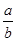 的值;
的值;
(2)求函数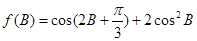 的值域.
的值域.
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.
在斜三角形 中,角A,B,C的对边分别为 a,b,c.
中,角A,B,C的对边分别为 a,b,c.
(1)若 ,求
,求 的值;
的值;
(2)若 ,求
,求 的值.
的值.
已知函数 ,
, ,
,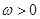 .
.
(1)求函数 的值域;
的值域;
(2)若函数 的最小正周期为
的最小正周期为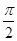 ,则当
,则当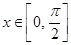 时,求
时,求 的单调递减区间.
的单调递减区间.
已知各项均为正数的等比数列 中,
中, .
.
(1)求公比 ;
;
(2)若 分别为等差数列
分别为等差数列 的第3项和第5项,求数列
的第3项和第5项,求数列 的通项公式.
的通项公式.