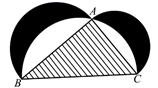
如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形 ABC的斜边 BC,直角边 AB, AC.△ ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III.在整个图形中随机取一点,此点取自I,II,III的概率分别记为 p 1, p 2, p 3,则( )
| A. |
p 1=p 2 |
B. |
p 1=p 3 |
| C. |
p 2=p 3 |
D. |
p 1=p 2+p 3 |
若函数 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足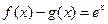 ,则有()
,则有()
A. |
B.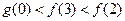 |
C. |
D.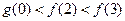 |
已知︱ ︱=1,︱
︱=1,︱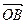 ︱=
︱=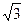 ,
,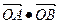 =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设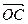 =m
=m +n
+n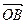 (m、n∈R),则
(m、n∈R),则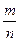 等于
等于
A.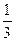 |
B.3 | C.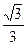 |
D.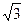 |
如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且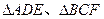 均为正三角形
均为正三角形 ,EF∥AB,EF=2,则该多面体的体积为
,EF∥AB,EF=2,则该多面体的体积为 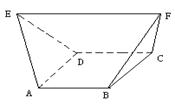
A.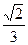 |
B.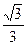 |
C.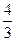 |
D.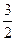 |
已知集合A={1,2,3,4,5},函数f(x)是A A的映射,若整数x+f(x)和整数x·f(x)的奇偶不同,那么满足条件的映射的个数为
A的映射,若整数x+f(x)和整数x·f(x)的奇偶不同,那么满足条件的映射的个数为
| A.15 | B.125 | C.1125 | D.21 |
设集合A={x∣∣x-a∣<1,x∈R}, B={x∣∣x-b∣>2,x∈R},若A B,则实数a、b必满足
B,则实数a、b必满足
| A.∣a+b∣≤3 | B.∣a+b∣≥3 | C.∣a-b∣≤3 | D.∣a-b∣≥3 |