已知函数 .
(1)讨论 的单调性;
(2)若 存在两个极值点 ,证明: .
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SA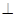 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN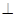 SC且交SC于点N.
SC且交SC于点N.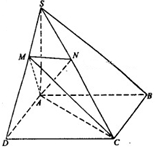
(Ⅰ)求证:SB∥平面ACM;
(Ⅱ)求证:平面SAC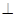 平面AMN.
平面AMN.
某校有教职工 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
(Ⅰ)随机抽取一人,是35岁以下的概率为 ,求
,求 的值;
的值;
(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为
(Ⅰ)叙述并证明正弦定理;
(Ⅱ)设 ,
, ,求
,求 的值.
的值.
已知在等比数列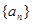 中,
中,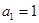 ,且
,且 是
是 和
和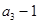 的等差中项.
的等差中项.
(Ⅰ)求数列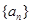 的通项公式;
的通项公式;
(Ⅱ)若数列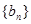 满足
满足 ,求
,求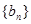 的前
的前 项和
项和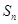 .
.
已知函数 ,
,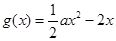 .
.
(Ⅰ)若曲线 在
在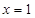 与
与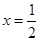 处的切线相互平行,求
处的切线相互平行,求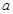 的值及切线斜率;
的值及切线斜率;
(Ⅱ)若函数 在区间
在区间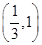 上单调递减,求
上单调递减,求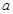 的取值范围;
的取值范围;
(Ⅲ)设函数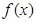 的图像C1与函数
的图像C1与函数 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.