(本小题满分15分)设等差数列 的前
的前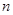 项和为
项和为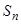 ,且
,且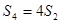 ,
,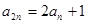 。
。


(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列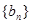 的前
的前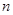 项和为
项和为 ,且
,且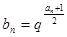 (其中
(其中 是非零的实数),若
是非零的实数),若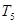 ,
,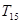 ,
,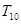 成等差数列,问
成等差数列,问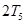 ,
,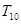 ,
,  能成等比数列吗?说明理由;
能成等比数列吗?说明理由;
(Ⅲ)设数列 的通项公式
的通项公式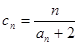 ,是否存在正整数
,是否存在正整数 、
、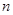 (
(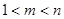 ),使得
),使得 ,
,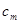 ,
,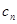
成等比数列?若存在,求出所有 、
、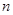 的值;若不存在,说明理由.
的值;若不存在,说明理由.
在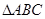 中,内角
中,内角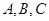 对边分别为
对边分别为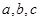 ,且
,且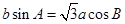 .
.
(Ⅰ)求角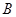 的大小;
的大小;
(Ⅱ)若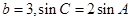 ,求
,求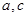 的值.
的值.
已知函数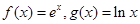 ,
,
(1)求证: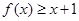 ;
;
(2)设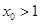 ,求证:存在唯一的
,求证:存在唯一的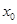 使得g(x)图象在点A(
使得g(x)图象在点A( )处的切线
)处的切线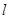 与y=f(x)图象也相切;
与y=f(x)图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得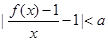 成立.
成立.
已知数列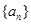 满足
满足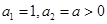 ,数列
,数列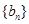 满足
满足
(1)若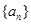 为等比数列,求
为等比数列,求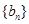 的前n项的和
的前n项的和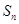 ;
;
(2)若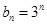 ,求数列
,求数列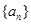 的通项公式;
的通项公式;
(3)若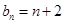 ,求证:
,求证: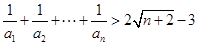
(本小题满分16分)已知椭圆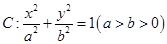 的离心率为
的离心率为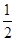 ,且过点
,且过点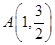 .
.
(1)求椭圆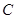 的方程;
的方程;
(2)若点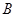 在椭圆上,点
在椭圆上,点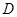 在
在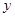 轴上,且
轴上,且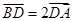 ,求直线
,求直线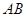 方程.
方程.
(本小题满分14分)小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售收入为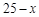 万元(国家规定大货车的报废年限为10年).
万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小张获得的年平均利润最大?(利润=累计收入+销售收入-总支出)