为等差数列 的前n项和,且 记 ,其中 表示不超过x的最大整数,如 .
(1)求 ;
(2)求数列 的前1 000项和.
(本小题满分12分)
已知函数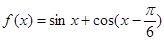 ,
,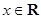 .
.
(1)求 的最大值;
的最大值;
(2)设△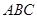 中,角
中,角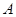 、
、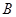 的对边分别为
的对边分别为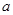 、
、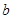 ,若
,若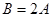 且
且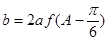 ,
,
求角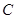 的大小.
的大小.
已知函数 .
.
(1)当a = 2时,求f (x) 的最小值;
(2)若f (x)在[1,e]上为单调减函数,求实数a的取值范围.
已知二次函数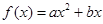 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为 ,
, .
.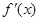 是
是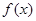 的导函数,且
的导函数,且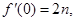
 .
.
(1)求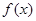 的表达式(含有字母
的表达式(含有字母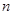 );
);
(2)若数列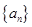 满足
满足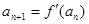 ,且
,且 ,求数列
,求数列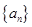 的通项公式;
的通项公式;
(3)在(2)条件下,若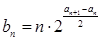 ,
,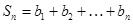 ,是否存在自然数
,是否存在自然数 ,使得当
,使得当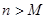 时
时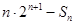
 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的 ;若不存在,说明理由.
;若不存在,说明理由.
(本小题满分14分)
已知椭圆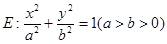 的左、右焦点分别为
的左、右焦点分别为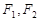 ,点
,点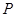 是
是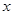 轴上方椭圆
轴上方椭圆 上的一点,且
上的一点,且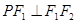 ,
,  ,
,  .
.
(1)求椭圆 的方程和
的方程和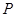 点的坐标;
点的坐标;
(2)判断以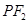 为直径的圆与以椭圆
为直径的圆与以椭圆 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.
如图,三角形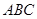 中,
中,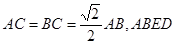 是边长为1的正方形,平面
是边长为1的正方形,平面 底面
底面 ,若
,若 分别是
分别是 的中点.
的中点.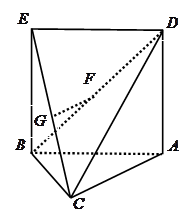
(1)求证: 底面
底面 ;
;
(2)求证: ⊥平面
⊥平面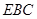 ;
;
(3)求几何体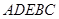 的体积
的体积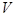 .
.