如下图,在正三棱柱 中, ,D是 的中点,点E在 上,且 。

(1)证明:平面 平面
(2)求直线 和平面 所成角的正弦值。
(本小题满分14分)已知圆C: ,
,
(1)求出此圆圆心C的坐标和半径r;
(2)求直线y=x被圆C所截得的弦长.
(本小题满分14分)已知x,y之间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(1)以x为横坐标,y为纵坐标在直角坐标系中画出散点图,并说明这两个变量之间的关系是正相关关系还是负相关关系。
(2)求线性回归方程.
(本小题满分14分)为了检测某条生产线上产品的尺寸。现从该条生产线上每隔一定时间取一件产品,共取了50件,测得其产品尺寸后,画得其频率分布直方图如下。
|

 内产品的个数.
内产品的个数.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是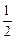 .
.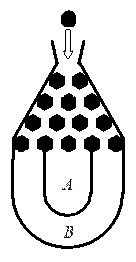
(Ⅰ)求小球落入 袋中的概率
袋中的概率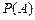 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记 为落入
为落入 袋中的小球个数,试求
袋中的小球个数,试求 的概率和
的概率和 的数学期望
的数学期望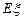 .
.
如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作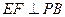 交
交 于
于

(1)求PF:FB的值
(2)求平面 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。