（本小题满分12分）已知数列{}的前n项和为，且满足．（Ⅰ）-优题课

（本小题满分12分）已知数列{}的前n项和为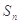，且满足．
（Ⅰ）证明：数列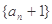为等比数列，并求数列{}的通项公式；
（Ⅱ）数列{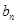}满足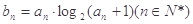，其前n项和为，试求满足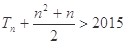的最小正整数n．

科目数学题型解答题难度中等

知识点：等比数列

求函数y=x⁴-2x²+5在区间［-2,2］上的最大值与最小值.

已知函数f(x)=x²e^-ax(a＞0),求函数在［1，2］上的最大值.

已知函数f(x)=x³+ax²+bx+c,曲线y=f(x）在点x=1处的切线为l:3x-y+1=0，若x=时，y=f(x）有极值.
（1）求a,b,c的值；
（2）求y=f(x）在［-3，1］上的最大值和最小值.

已知函数 $f (x) = \frac{1}{(1 - x)^{n}} + + a \ln (x - 1)$ ,其中 $n \in N^{*}$ , $a$ 为常数.
(1)当 $n = 2$ 时,求函数 $f (x)$ 的极值;
(2)当 $a = 1$ 时,证明:对任意的正整数 $n$ ,当 $x \geq 2$ 时,有 $f (x) \leq x - 1$ .

设函数f（x）=（x＞0且x≠1）.
（1）求函数f（x）的单调区间；
（2）已知2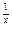＞x^a对任意x∈（0，1）成立，求实数a的取值范围.

试卷网试题网古诗词网作文网范文网