已知函数
,其中
,
为常数.
(1)当
时,求函数
的极值;
(2)当
时,证明:对任意的正整数
,当
时,有
.
已知二次函数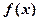 满足:①若
满足:①若 时有极值;②图像过点
时有极值;②图像过点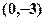 ,且在该点处的切线与直线
,且在该点处的切线与直线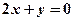 平行.
平行.
(1)求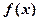 的解析式;
的解析式;
(2)若曲线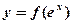 上任意一点
上任意一点 的切线斜率恒大于
的切线斜率恒大于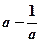 ,求
,求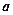 的取值范围;
的取值范围;
(3)求函数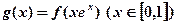 的值域.
的值域.
定义在R上的单调函数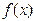 满足
满足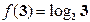 ,且对于任意的
,且对于任意的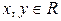 ,
,
都有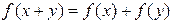 .
.
(1)求证: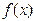 为奇函数;
为奇函数;
(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数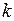 的取值范围.
的取值范围.
(本小题满分12分)
设命题p:函数 是R上的减函数,命题q: 函数
是R上的减函数,命题q: 函数 在
在 的值域是
的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求
[-1,3].若“p且q”为假命题。“p或q” 为真命题,求 的取值范围
的取值范围
(本小题满分10分)设全集是实数集R ,集合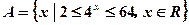 ,集合
,集合 ,
,
(1) 当  时 ,求
时 ,求 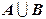 ;
;
(2) 若 ,求实数
,求实数 的取值范围.
的取值范围.
已知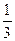 ≤
≤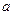 ≤1,若函数
≤1,若函数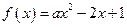 在区间[1,3]上的最大值
在区间[1,3]上的最大值
为 ,最小值为
,最小值为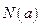 ,令
,令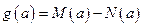 .
.
(1)求 的函数表达式;
的函数表达式;
(2)判断函数 在区间[
在区间[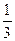 ,1]上的单调性,并求出
,1]上的单调性,并求出 的最小值 .
的最小值 .