定义在R上的单调函数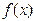 满足
满足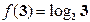 ,且对于任意的
,且对于任意的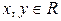 ,
,
都有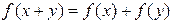 .
.
(1)求证: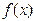 为奇函数;
为奇函数;
(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数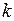 的取值范围.
的取值范围.
型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系,随机抽取了189名员工进行调查,其中支持企业改革的调查者中,工作积极的54人,工作一般的32人,而不太赞成企业改革的调查者中,工作积极的40人,工作一般的63人.
(1)根据以上数据建立一个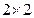 的列联表;
的列联表;
(2)对于人力资源部的研究项目,根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系?
附表:
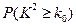 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
设 求证:
求证: (用两种方法证明).
(用两种方法证明).
用三段论证明:通项为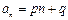 (
( 为常数)的数列
为常数)的数列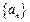 是等差数列.
是等差数列.
(本题满分15分)已知a∈R,函数f (x) =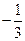 x3 +
x3 +  ax2 + 2ax (x∈R).(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;(Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由;(Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
ax2 + 2ax (x∈R).(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;(Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由;(Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
(本小题满分14分)
已知函数 对于任意
对于任意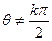 (
(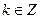 ),都有式子
),都有式子 成立(其中
成立(其中 为常数).
为常数).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)利用函数 构造一个数列,方法如下:
构造一个数列,方法如下:
对于给定的定义域中的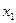 ,令
,令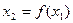 ,
, ,…,
,…,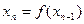 ,…
,…
在上述构造过程中,如果 (
(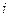 =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(ⅰ)如果可以用上述方法构造出一个常数列,求 的取值范围;
的取值范围;
(ⅱ)是否存在一个实数 ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为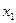 ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(ⅲ)当 时,若
时,若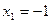 ,求数列
,求数列 的通项公式.
的通项公式.