已知函数f(x)=x2e-ax(a>0),求函数在[1,2]上的最大值.
已知各项均为正数的数列{ }的前n项和满足
}的前n项和满足 ,且
,且
(1)求{ }的通项公式;
}的通项公式;
(2)设数列{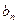 }满足
}满足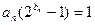 ,并记
,并记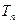 为{
为{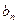 }的前n项和,求证:
}的前n项和,求证:
已知实数列 等比数列,其中
等比数列,其中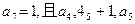 成等差数列.
成等差数列.
(1)求数列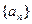 的通项公式;
的通项公式;
(2)数列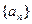 的前
的前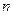 项和记为
项和记为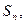 证明:
证明: 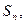 <128
<128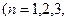 …).
…).
在数列 中,
中,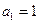 ,
, .
.
(1)设 .证明:数列
.证明:数列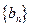 是等差数列;
是等差数列;
(2)求数列 的前
的前 项和
项和 .
.
如图, PA⊥平面ABCD,四边形ABCD是矩形,点E在边AB上,F为PD的中点,AF∥平面PCE,二面角P-CD-B为450,AD=2,CD=3.
(1)试确定E点位置; (2)求直线AF到平面PCE的距离.
设数列{an}的前n项和为Sn=2n+1-2,{bn }是公差不为0的等差数列,其中b2、b4、b9依次成等比数列,且a2=b2
(1)求数列{an }和{bn}的通项公式: (2)设cn= ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn