设 是首项为 ,公差为 的等差数列, 是首项 ,公比为q的等比数列
(1) 设 若 对n=1,2,3,4均成立,求d的取值范围
(2) 若 , , 证明:存在 ,使得 对n=2,3,…, 均成立,并求 的取值范围(用 表示)。
(本题12分)
设命题P:函数 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数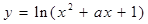 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
(本题12分)
已知函数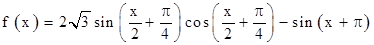 。
。
(1)求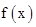 的最小正周期;
的最小正周期;
(2)若将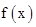 的图象按向量
的图象按向量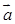 =(
=(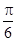 ,0)平移得到函数g(x)的图象,求函数g(x)在区间
,0)平移得到函数g(x)的图象,求函数g(x)在区间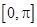 上的最大值和最小值。
上的最大值和最小值。
(本小题14分)设函数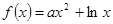 .
.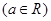
(Ⅰ)讨论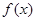 的单调性;
的单调性;
(Ⅱ)已知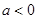 ,若函数
,若函数 的图象总在直线
的图象总在直线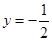 的下方,求
的下方,求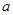 的取值范围;
的取值范围;
(Ⅲ)记 为函数
为函数 的导函数.若
的导函数.若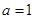 ,试问:在区间
,试问:在区间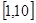 上是否存在
上是否存在 (
(
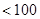 )个正数
)个正数 …
… ,使得
,使得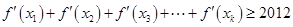 成立?请证明你的结论.
成立?请证明你的结论.
(本小题12分)椭圆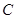 :
: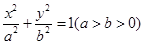 的两个焦点为
的两个焦点为 ,点
,点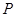 在椭圆
在椭圆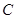 上,且
上,且 .
.
(Ⅰ)求椭圆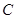 的方程;
的方程;
(Ⅱ)若直线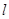 过圆
过圆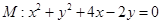 的圆心,交椭圆
的圆心,交椭圆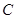 于
于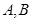 两点,且
两点,且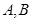 关于点
关于点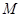 对称,求直线
对称,求直线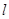 的方程。
的方程。
(本小题12分)某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入 万元,每件产品的成本将降低
万元,每件产品的成本将降低 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少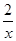 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(Ⅰ)求 的函数解析式;
的函数解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时 的值.
的值.