为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10。把这6名学生的得分看成一个总体。(1)求该总体的平均数;(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本。求该样本平均数与总体平均数之差的绝对值不超过0.5的概率。
(本小题满分14分)如图所示,在棱长为2的正方体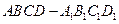 中,
中, 、
、 分
分
别为 、
、 的中点.
的中点.
(Ⅰ)求证: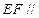 平面
平面 ;
;
(Ⅱ)求证: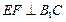 ;
;
(III)求三棱锥 的体积.
的体积.
(本小题满分13分)
已知椭圆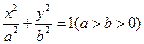 的左焦点为
的左焦点为 ,左右顶点分别为
,左右顶点分别为 ,上顶点为
,上顶点为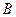 ,过
,过 三点作圆
三点作圆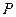 ,其中圆心
,其中圆心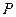 的坐标为
的坐标为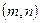 .
.
(Ⅰ)当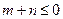 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.
(Ⅱ)直线 能否和圆
能否和圆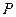 相切?证明你的结论.
相切?证明你的结论.
(本小题满分12分)
同时掷两个骰子,计算:
(Ⅰ)一共有多少种不同的结果?
(Ⅱ)其中向上的点数之和是5的结果有多少种?概率是多少?
(III)向上的点数之和小于5的概率是多少?
(本小题满分13分)
已知在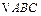 中,
中,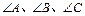 所对的边分别为
所对的边分别为 ,若
,若 且
且
(Ⅰ)求角A、B、C的大小;
(Ⅱ)设函数 ,求函数
,求函数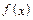 的单调递增区间,并指出它相邻两对称轴间的距离.
的单调递增区间,并指出它相邻两对称轴间的距离.
(本小题满分14分)设圆 ,将曲线上每一点的纵坐标压缩到原来的
,将曲线上每一点的纵坐标压缩到原来的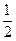 ,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线
,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交曲线C于A、B两个不同点.
交曲线C于A、B两个不同点.
(1)求曲线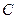 的方程;
的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.