如图,在四棱锥
中,
,且
.

(1)证明:平面 平面 ;
(2)若 , ,求二面角 的余弦值.
(本小题满分13分)
已知数列{an}的前n项和为Sn,Sn=2-(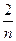 +1)an(n≥1).
+1)an(n≥1).
(1)求证:数列{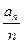 }是等比数列;
}是等比数列;
(2)设数列{2nan}的前n项和为Tn,An= .试比较An与
.试比较An与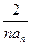 的大小。
的大小。
(本小题满分13分)
某建筑工地在一块长AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为 米。
米。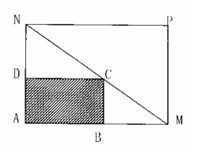
(1)要使矩形学生公寓ABCD的面积不小于144平方米,AB的长度应在什么范围?
(2)长度AB和宽度AD分别为多少米时矩形学生公寓ABCD的面积最大?最大值是多少平方米?
(本小题满分12分)
如图,在三棱柱ADF—BCE中,侧棱 底面
底面 ,底面
,底面 是等腰直角三角形,且
是等腰直角三角形,且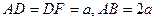 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点. 
(1)求证GA∥平面FMC;
(2)求直线DM与平面ABEF所成角。
(本小题满分12分)
盒中有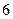 个小球,
个小球,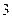 个白球,记为
个白球,记为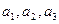 ,
,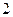 个红球, 记为
个红球, 记为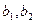 ,
, 个黑球, 记为
个黑球, 记为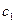 ,除了颜色和编号外,球没有任何区别.
,除了颜色和编号外,球没有任何区别.
(1) 求从盒中取一球是红球的概率;
(2) 从盒中取一球,记下颜色后放回,再取一球,记下颜色,若取白球得 分,取红球得
分,取红球得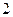 分,取黑球得
分,取黑球得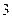 分,求两次取球得分之和为
分,求两次取球得分之和为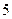 分的概率
分的概率
(本小题满分12分)
已知函数 .
.
(1)求函数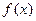 的最小正周期;
的最小正周期;
(2)当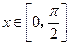 时,求函数
时,求函数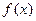 的取值范围.
的取值范围.