已知函数 , ,其中 是自然对数的底数.
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)令 ,讨论 的单调性并判断有无极值,有极值时求出极值.
已知函数

(1)利用“五点法”画出该函数在长度为一个周期上的简图;
列表;
 |
|||||
 |
|||||
 |
作图:
(2)说明该函数的图像可由 的图像经过怎样的变换得到.
的图像经过怎样的变换得到.
已知 是一个平面内的三个向量,其中
是一个平面内的三个向量,其中 =(1,2)
=(1,2)
(1)若| |=
|= ,
, ∥
∥ ,求
,求 及
及 ·
· .
.
(2)若|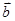 |=
|= ,且
,且 +2
+2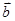 与3
与3 -
-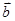 垂直,求
垂直,求 与
与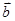 的夹角.
的夹角.
(1)求值:
(2)已知 值.
值.
已知函数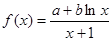 在点
在点 处的切线方程为
处的切线方程为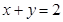 .
.
(I)求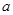 ,
,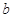 的值;
的值;
(II)对函数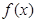 定义域内的任一个实数
定义域内的任一个实数 ,
,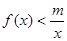 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| 男性 |
女性 |
合计 |
|
| 反感 |
10 |
||
| 不反感 |
8 |
||
| 合计 |
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是 .
.
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(
当 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.