已知点 ,圆C:
,圆C: 与椭圆E:
与椭圆E: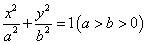 有一个公共点
有一个公共点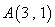 ,
,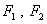 分别是椭圆的左、右焦点,直线
分别是椭圆的左、右焦点,直线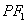 与圆C相切.
与圆C相切.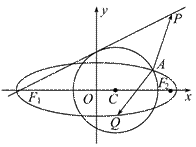
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求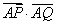 的取值范围.
的取值范围.
如图,动点 与两定点
与两定点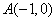 、
、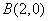 构成
构成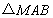 ,且
,且 ,设动点
,设动点 的轨迹为
的轨迹为 .
.
(1)求轨迹 的方程;
的方程;
(2)设直线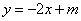 与
与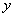 轴相交于点
轴相交于点 ,与轨迹
,与轨迹 相交于点
相交于点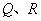 ,且
,且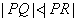 ,求
,求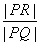 的取值范围.
的取值范围.
已知双曲线的中心在原点,离心率为2,一个焦点为F(-2,0).
(1)求双曲线方程;
(2)设Q是双曲线上一点,且过点F,Q的直线l与y轴交于点M,若 = 2
= 2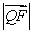 ,求直线l的方程.
,求直线l的方程.
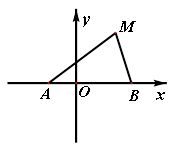
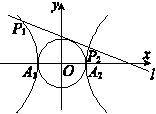
如图,已知双曲线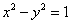 的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆
的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆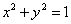 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为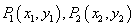 .
.
(1)求k的取值范围,并求 的最小值;
的最小值;
(2)记直线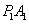 的斜率为
的斜率为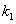 ,直线
,直线 的斜率为
的斜率为 ,那么
,那么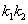 是定值吗?证明你的结论.
是定值吗?证明你的结论.
设 是首项为
是首项为 ,公差为
,公差为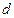 的等差数列(d≠0),
的等差数列(d≠0),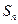 是其前
是其前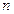 项和.记bn=
项和.记bn=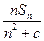 ,
, ,其中
,其中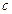 为实数.
为实数.
(1) 若 ,且
,且 ,
, ,
, 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+);
(2) 若 是等差数列,证明:
是等差数列,证明: .
.