已知函数 .
(Ⅰ)求曲线 的斜率为1的切线方程;
(Ⅱ)当 时,求证: ;
(Ⅲ)设 ,记 在区间 上的最大值为 ,当 最小时,求 的值.
要从12人中选出5人参加一项活动,其中A、B、C 3人至多2人入选,有多少种不同选法?
已知函数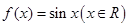 与
与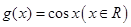 .
.
(1)对于函数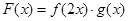 ,有下列结论:①
,有下列结论:①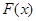 是奇函数;②
是奇函数;②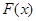 是周期函数,最小正周期为
是周期函数,最小正周期为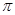 ;③
;③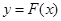 的图象关于点
的图象关于点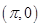 对称;④
对称;④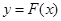 的图象关于直线
的图象关于直线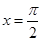 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
(2)对于函数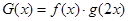 ,求满足
,求满足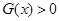 的
的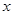 的取值范围;
的取值范围;
(3)设函数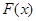 的值域为
的值域为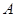 ,函数
,函数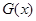 的值域为
的值域为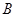 ,试判断集合
,试判断集合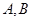 之间的关系.
之间的关系.
已知函数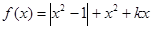 .
.
(1)若对于区间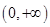 内的任意
内的任意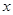 ,总有
,总有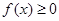 成立,求实数
成立,求实数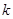 的取值范围;
的取值范围;
(2)若函数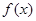 在区间
在区间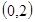 内有两个不同的零点
内有两个不同的零点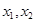 ,求:
,求:
①实数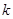 的取值范围; ②
的取值范围; ②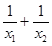 的取值范围.
的取值范围.
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间
与时间 小时
小时 间的关系为
间的关系为 .如果在前
.如果在前 个小时消除了
个小时消除了 的污染物,试求:
的污染物,试求:
(1) 个小时后还剩百分之几的污染物?
个小时后还剩百分之几的污染物?
(2)污染物减少 所需要的时间.(参考数据:
所需要的时间.(参考数据: )
)
已知函数 。
。
(1)求函数 的单调递减区间;
的单调递减区间;
(2)求函数 在区间
在区间 上的最大值及最小值;
上的最大值及最小值;
(3)将函数 的图象作怎样的变换可得到
的图象作怎样的变换可得到 的图象?
的图象?