某农谷生态园响应国家发展有机农业政策，大力种植有机蔬菜，某超市看好甲、乙两种有机蔬菜的市场价值，经调查甲种蔬菜进价每千克 元，售价每千克 16 元；乙种蔬菜进价每千克 元，售价每千克 18 元．
（ 1 ）该超市购进甲种蔬菜 10 千克和乙种蔬菜 5 千克需要 170 元；购进甲种蔬菜 6 千克和乙种蔬菜 10 千克需要 200 元．求 ， 的值．
（ 2 ）该超市决定每天购进甲、乙两种蔬菜共 100 千克，且投入资金不少于 1160 元又不多于 1168 元，设购买甲种蔬菜 千克，求有哪几种购买方案．
（ 3 ）在（ 2 ）的条件下，超市在获得的利润取得最大值时，决定售出的甲种蔬菜每千克捐出 元，乙种蔬菜每千克捐出 元给当地福利院，若要保证捐款后的利润率不低于 20% ，求 的最大值．
关于x的一元二次方程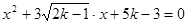
，问：是否存在整数k使方程有两个不相等的实数根，若存在，请求出k的值并求出此时方程的两个实数根；若不存在，试说明理由．
（1）计算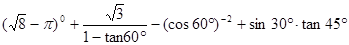
；
（2）解方程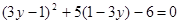 
如图，在直角坐标系中，半径为1的⊙A圆心与原点O重合，直线l分别交x轴、y轴于点B、C，若点B的坐标为(6，0)，tan∠ABC=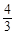
．
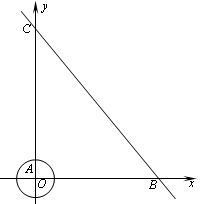
（1）若点P是⊙A上的动点，求P到直线BC的最小距离，并求此时点P的坐标；
（2）若点A从原点O出发，以1个单位/秒的速度沿着线路OB→BC→CO运动，回到点O停止运动，⊙A随着点A的运动而移动．设点A运动的时间为t．
①求⊙A在整个运动过程中与坐标轴相切时t的取值；
②求⊙A在整个运动过程中所扫过的图形的面积为．
施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．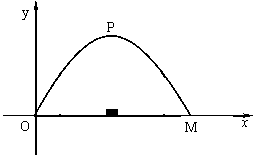
（1）求出这条抛物线的函数解析式，并写出自变量x的取值范围；
（2）隧道下的公路是双向等宽行车道(正中间是一条宽1米的隔离带)，其中的一条行车道能否行驶宽2.5米、高5米的特种车辆？请通过计算说明；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上．B、C点在地面OM线上（如图所示）．为了筹备材料，需求出“脚手架”三根钢管AB、AD、DC的长度之和的最大值是多少，请你帮施工队计算一下．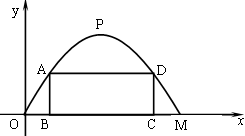
西瓜经营户以2元/kg的价格购进一批小型西瓜，以3元/kg的价格出售，每天可售出200kg．为了尽快售罄，该经营户决定降价促销，经调查发现，这种小型西瓜每降价0.1元/kg，每天可多售出40kg．另外，经营期间每天还需支出固定成本24元．该经营户要想每天至少盈利200元，应将每千克小型西瓜的售价降低多少元？