如图 ① ,直线 经过点 且平行于 y 轴,二次函数 的图象经过点 ,交直线 于点 N ,图象的顶点为 D ,它的对称轴与 x 轴交于点 C ,直线 DM 、 DN 分别与 x 轴相交于 A 、 B 两点.
( 1 )当 时,求点 N 的坐标及 的值;
( 2 )随着 a 的变化, 的值是否发生变化?请说明理由;
( 3 )如图 ② , E 是 x 轴上位于点 B 右侧的点, , DE 交抛物线于点 F .若 ,求此时的二次函数表达式.

(年江苏盐城12分)如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数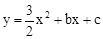 的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当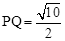 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)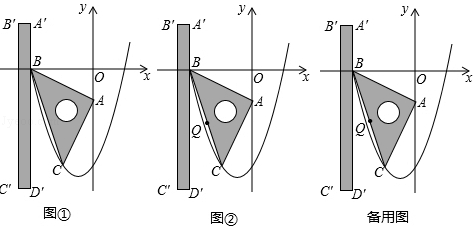
(年甘肃天水12分)如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=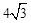 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME的度数.
(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.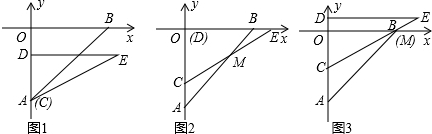
(年陕西省10分)已知抛物线C:y=﹣x2+bx+c经过A(﹣3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.
(1)求抛物线C的表达式;
(2)求点M的坐标;
(3)将抛物线C平移到C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?
(年山西省13分)综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(﹣2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.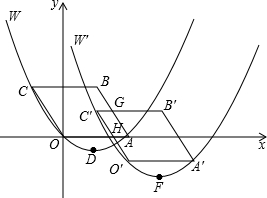
(1)求抛物线W的解析式及顶点D的坐标;
(2)将抛物线W和 OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和
OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和 O′A′B′C′,在向下平移的过程中,设
O′A′B′C′,在向下平移的过程中,设 O′A′B′C′与
O′A′B′C′与 OABC的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
OABC的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线W′的顶点为F,若点M是x轴上的动点,点N时抛物线W′上的动点,试判断是否存在这样的点M和点N,使得以D、F、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(年四川泸州12分)如图,已知一次函数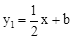 的图象l与二次函数
的图象l与二次函数 的图象
的图象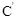 都经过点B(0,1)和点C,且图象
都经过点B(0,1)和点C,且图象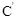 过点A(
过点A( ,0).
,0).
(1)求二次函数的最大值;
(2)设使 成立的x取值的所有整数和为s,若s是关于x的方程
成立的x取值的所有整数和为s,若s是关于x的方程 的根,求a的值;
的根,求a的值;
(3)若点F、G在图象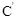 上,长度为
上,长度为 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P 的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P 的坐标.