在△ABC中, ,D为△ABC内一点,连接BD,DC,延长DC到点E,使得 .
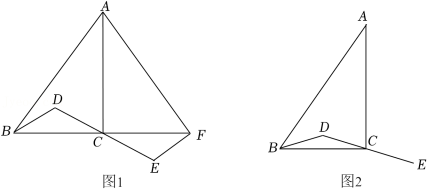
(1)如图1,延长BC到点F,使得 ,连接AF,EF.若 ,求证: ;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图2.若 ,用等式表示线段CD与CH的数量关系,并证明.
(本题满分12分) 为了让广大青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动可以锻炼人的灵活性,增强人的爆发力.因此小明和小亮在课外活动中报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补齐下面的表格;
| 第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
|
| 小明 |
13.3 |
13.4 |
13.3 |
13.3 |
|
| 小亮 |
13.2 |
13.1 |
13.5 |
13.3 |
(2)分别计算他们的平均数、极差和方差填入下表,若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
| 平均数 |
极差 |
方差 |
|
| 小明 |
13.3 |
0.004 |
|
| 小亮 |
0.4 |
如图,BD是直径,过⊙O上一点A作⊙O切线交DB延长线于P,过B点作BC∥PA交⊙O于C,连接AB、AC ,
(1)求证:AB = AC
(2)若PA=" 10" ,PB =" 5" ,求⊙O半径.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90
 ,求证四边形DEBF是菱形.
,求证四边形DEBF是菱形.
如图,直线 和抛物线
和抛物线 都经过点A(1,0),B(a,2).
都经过点A(1,0),B(a,2).
⑴求直线和抛物线的解析式;
⑵当x为何值时,
 (直接写出答案).
(直接写出答案).
三角形两边长分别是8和6,第三边的长是一元二次方程x2-16x+60=0的一个实数根,求此三角形的面积.