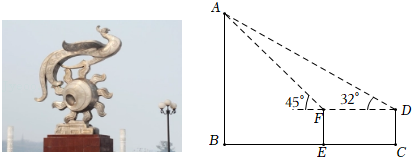
荆州城徽“金凤腾飞”立于古城东门外.如图,某校学生测量其高 (含底座),先在点 处用测角仪测得其顶端 的仰角为 ,再由点 向城徽走 到 处,测得顶端 的仰角为 .已知 三点在同一直线上,测角仪离地面的高度 ,求城徽的高 .(参考数据: ).
(年山东潍坊12分)经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为O千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时时,应控制大桥上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
(年江苏扬州12分)某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装,专卖店又缺少资金. “中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示. 该店支付员工的工资为每人每天82元,每天还应该支付其它费用为106元(不包含债务).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还债务,当某天的销售价为48元/件时,当天正好收支平衡(收入=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元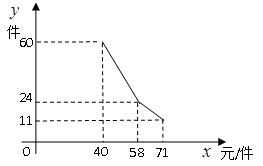
(年江苏无锡10分)某发电厂共有6台发电机发电,每台的发电量为300万千瓦/月.该厂计划从今年7月开始到年底,对6台发电机各进行一次改造升级.每月改造升级1台,这台发电机当月停机,并于次月再投入发电,每台发电机改造升级后,每月的发电量将比原来提高20%.已知每台发电机改造升级的费用为20万元.将今年7月份作为第1个月开始往后算,该厂第x(x是正整数)个月的发电量设为y(万千瓦).
(1)求该厂第2个月的发电量及今年下半年的总发电量;
(2)求y关于x的函数关系式;
(3)如果每发1千瓦电可以盈利0.04元,那么从第1个月开始,至少要到第几个月,这期间该厂的发电盈利扣除发电机改造升级费用后的盈利总额ω1(万元),将超过同样时间内发电机不作改造升级时的发电盈利总额ω2(万元)?
(年湖南湘西12分)湘西盛产椪柑,春节期间,一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆部不少于3辆.
(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 椪柑品种 |
A |
B |
C |
| 每辆汽车运载量 |
10 |
8 |
6 |
| 每吨椪柑获利(元) |
800 |
1200 |
1000 |
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少椪柑积压,湘西州制定出台了促进椪柑销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销客户,按每吨50元的标准实行运费补贴.若要使该外地运销客户所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
(年湖南怀化10分)设m是不小于﹣1的实数,使得关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x 1,x2.
(1)若 ,求
,求 的值;
的值;
(2)求 的最大值.
的最大值.