如图(Ⅰ)所示,某登山运动爱好者由山坡①的山顶点A处沿线段 至山谷点 处,再从点 处沿线段 至山坡②的山顶点B处.如图(Ⅱ)所示,将直线 视为水平面,山坡①的坡角 ,其高度 为 千米,山坡②的坡度 , 于 ,且 千米.
(1)求 的度数;
(2)求在此过程中该登山运动爱好者走过的路程.

计算 的结果为
A. B. C. D.
如图,将正方形 折叠,使顶点 与 边上的一点 重合 不与端点 , 重合),折痕交 于点 ,交 于点 ,边 折叠后与边 交于点 .设正方形 的周长为 , 的周长为 ,则 的值为
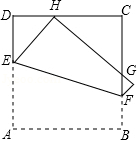
A. B.
C. D.随 点位置的变化而变化
中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第六天走的路程为
A.24里B.12里C.6里D.3里
如图,菱形 的对角线 , 的长分别为 , ,则这个菱形的周长为
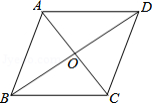
A. B. C. D.
如图,已知直线 ,直线 分别与 , 相交, ,则 的度数为

A. B. C. D.