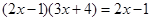如图,在 中, ,点 是 边的中点,点 在 边上, 经过点 且与 边相切于点 , .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的长.

已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: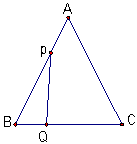
(1)求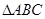 的面积;
的面积;
(2)当t为何值是,△PBQ是直角三角形?
(3)设四边形APQC的面积为y(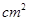 ),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是
),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是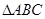 面积的三分之二?如果存在,求出t的值;不存在请说明理由.
面积的三分之二?如果存在,求出t的值;不存在请说明理由.
某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(用含x的代数式表示)
(2)如果批发商希望通过销售这批T恤获利8750元,那么第二个月的单价应是多少元?
(3)要使批发商获利最多,那么第二个月的单价应是多少元,此时获得的最大利润是多少元?请说明理由,并写出必要的过程.
为了进一步了解光明中学八年级学生的身体素质情况,体育老师以八年级(1)班50位学生为样本进行了一分钟跳绳次数测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图(如下所示):
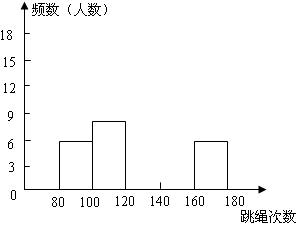
请结合图表完成下列问题:
(1)表中的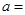 ;
;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)已知该校八年级共有学生800,请你估计一分钟跳绳次数不低于120次的八年级学生大约多少名?
证明命题“等腰三角形底边上的中点到两腰的中点距离相等”。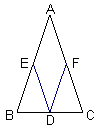
已知:在△ABC中,_____________________________
求证:____________________
证明:
(1)计算: ①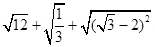 ;②
;②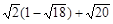 ÷
÷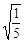
(2)解方程:①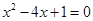 ;②
;②