已知二次函数 的图象经过两点 .
(1)如果 都是整数,且 ,求 的值;
(2)设二次函数 的图象与 轴的交点为 ,与 轴的交点为 .如果关于 的方程 的两个根都是整数,求 的面积.
站在水平高度为h米的地方看到可见的水平距离为d米,它们近似地符号公式为 。某一登山者从海拔n米处登上海拔2n米高的山顶,那么他看到的水平线的距离是原来的多少倍?
。某一登山者从海拔n米处登上海拔2n米高的山顶,那么他看到的水平线的距离是原来的多少倍?
化简:
(1)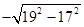 (2)
(2)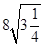 (3)
(3) (4)
(4)
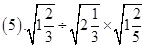
已知: 求
求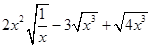 的值。
的值。
阅读材料:形如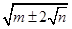 的化简,只要我们找到两个正数a、b,使得
的化简,只要我们找到两个正数a、b,使得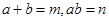 ,使得
,使得 ,那么,便有
,那么,便有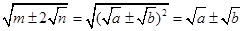 (a>b).例如:化简
(a>b).例如:化简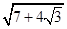 .
.
解:首先把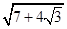 化为
化为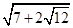 ,这里m=7,n=12;
,这里m=7,n=12;
由于4+3=7,4×3=12,即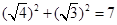 ,
,
∴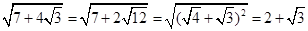 .
.
根据上述阅读材料中例题的方法,化简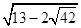 .
.
观察下列各式及其验证过程 ,验证:
,验证: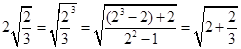 ;
;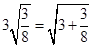 ,验证:
,验证: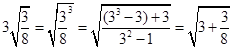 .
.
(1)按上述两个等式及其验证过程的基本思路,猜想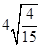 的变形结果,并进行验证;
的变形结果,并进行验证;
(2)针对上式各式反应的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.