如图,在平面直角坐标系 中,抛物线 与两坐标轴分别相交于 三点.
(1)求证: ;
(2)点 是第一象限内该抛物线上的动点,过点 作 轴的垂线交 于点 ,交 轴于点 .
①求 的最大值;
②点 是 的中点,若以点 为顶点的三角形与 相似,求点 的坐标.

两架轧钢机同时工作8小时,轧出一定数量的钢板.若单用其中第一架轧钢机轧出同样数量的钢板,要比单用第二架轧钢机轧出同样数量的钢板多用3.6小时,求每架轧出这些钢板所需的时间.
据报道,全国硕士研究生2011年入学考试报考人数再一次达到历史高峰,以下是根据2008年——2011年全国硕士研究生报考人数绘制的统计图.
(1)请你根据统计图计算出2009年——2011年这三年全国硕士研究生入学考试报考人数比上年增加值的平均数为万人(结果保留整数);
(2)为了调查各专业报考人数,某网站进行了网上调查,并将调查结果绘制成扇形统计图,请你补全扇形统计图并计算图中表示金融专业的扇形的圆心角为
度;若2012年全国硕士研究生报考人数按照(1)中的平均数增长,各专业报考人数所占比例与2011年相比基本保持不变,请你预测2012年全国硕士研究生入学考试报考金融专业的考生约有万人(结果保留整数).
如图,在△ABC中,∠ B=90°,AB=6cm,BC=8cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.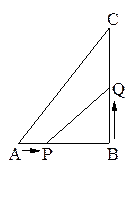
(1)如果P、Q分别从A、B同时出发,经过多长时间,使△PBQ的面积为8cm2?
(2)如果P、Q分别从A、B同时出发, 当P、Q两点运动几秒时,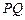 有最小值,并求这个最小值.
有最小值,并求这个最小值.
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.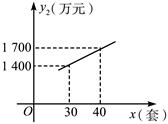
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
如图所示, 是直角三角形,
是直角三角形, ,以
,以 为直径的⊙O交
为直径的⊙O交 于点
于点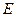 ,点
,点 是
是 边的中点,连结
边的中点,连结 .
.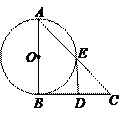
(1)求证: 与⊙O相切;
与⊙O相切;
(2)若⊙O的半径为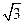 ,
, ,求
,求 .
.