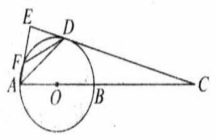
如图,点 在以 为直径的 上,过 作 的切线交 的延长线于点 于点 ,交 于点 ,连接 .
(1)求证:
(2)求证: ;
(3)若 ,求 的长.
如图,在菱形ABCD中,点E,F分别为边BC,CD的中点,连接AE,AF.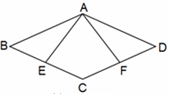
求证:△ABE≌△ADF.
(1)计算: ;
;
(2)化简: .
.
如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0)若抛物线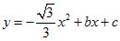 过A.B两点.
过A.B两点.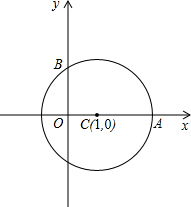
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PBO=∠POB? 若存在求出P的坐标,不存在说明理由;
(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB面积为S,求S的最大(小)值.
如图,已知直线PA交⊙O于A.B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CDPA⊥,垂足为D. 
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
如图,平行四边形ABCD中, ,点
,点 的坐标是
的坐标是 ,以点
,以点 为顶点的抛物线
为顶点的抛物线 经过
经过 轴上的点
轴上的点 .
.
(1)求点 的坐标;
的坐标;
(2)若抛物线向上平移后恰好经过点 ,求平移后抛物线的解析式.
,求平移后抛物线的解析式.