如图①,在, 中,以下是小亮探究 与 之间关系的方法:
根据你掌握的三角函数知识.在图②)的锐角 中,探究 之间的关系,并写出探究过程.

已知 是最小的正整数,b、c互为倒数,|b|+b=0,|c|=
是最小的正整数,b、c互为倒数,|b|+b=0,|c|= ,求式子
,求式子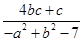 的值。
的值。
如图①所示的是一个长为2m,宽是2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形。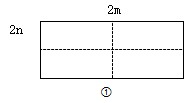

(1)你认为图‚中的阴影部分的正方形的边长等于_______。
(2)请用两种不同的方法列代数式表示图‚中的阴影部分的面积。
方法______________
方法‚______________
(3)观察图,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
(4)当若m+n=6,mn=8,求(m-n)2的值.求阴影部分的面积。
计算:-32× -2[(-5)2×(-
-2[(-5)2×(- )-240÷(-4)×
)-240÷(-4)×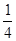 -2]
-2]
计算:(-3)3÷2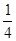 ×(-
×(- )2+4-22×(-
)2+4-22×(- )
)
计算: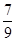 ×{
×{ [2×(-1)3-7]-18}-(3×
[2×(-1)3-7]-18}-(3× )2
)2