如图，设 为等腰直角三角形 斜边 上任意一点， 于点 于点 于 点， 交 于点 ，延长 并在其延长线上取一点 ，使得 .求证： ，且 .
如图，斜坡AC的坡度（坡比）为1:
，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．
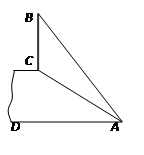
如图，矩形ABCD内接于⊙O，且AB＝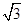
，BC＝1，求图中阴影部分所表示的扇形OAD的面积．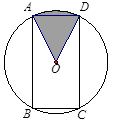
如图，已知A（-4，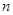
），B（2，-4）是一次函数
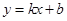的图象和反比例函数
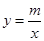的图象的两个交点．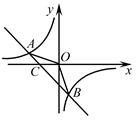
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与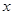
轴的交点C的坐标及△AOB的面积；
（3）当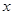取何值时，反比例函数值大于一次函数值．
（1）已知：sinα·cos60º＝
，求锐角α；
（2）计算：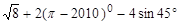
．
如图，抛物线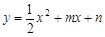
与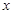
轴交于A、B两点，与
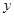轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.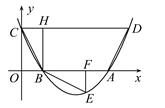
（1）求C点的坐标及抛物线的解析式；
（2）将△BCH绕点B按顺时针旋转90º后再沿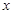轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；
（3）设过点E的直线交AB边于点P，交CD边于点Q. 问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.