某造纸厂有甲和乙两个长方体蓄水池，将甲蓄水池中的水以每小时 的速度注人乙蓄水池．甲、乙两个蓄水池中水的深度 与注水时间 的函数关系如图所示．结合图象回答下列问题：
（1）分别求出甲蓄水池和乙蓄水池中水的深度 与注水时间 之间的函数关系式（不必写出 的取值范围）；
（2）求注水多长时间甲蓄水池和乙蓄水池中水的深度相同；
（3）求注水多长时间甲、乙两个蓄水池的蓄水量相同．
如图，在平面直角坐标系
中，直线AB与
轴交于点A，与
轴交于点C（
，
），且与反比例 函数
在第一象限内的图象交于点B，且BD⊥
轴于点D，OD
．
（1）求直线AB的函数解析式；
（2）设点P是轴上的点，若△PBC的面积等于
，直接写出点P的坐标．
先化简
，然后在不等式
＞
的非负整数解中选一个使原式有意义的数代入求值．
如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．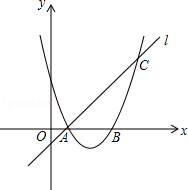
（1）求抛物线的解析式；
（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；
（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．
如图，已知⊙O的半径为4，CD是⊙O的直径，AC为⊙O的弦，B为CD延长线上的一点，∠ABC=30°，且AB=AC．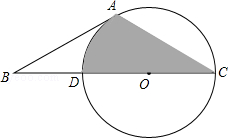
（1）求证：AB为⊙O的切线；
（2）求弦AC的长；
（3）求图中阴影部分的面积．
佳佳果品店在批发市场购买某种水果销售，第一次用1200元购进若干千克，并以每千克8元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了10%，用1452元所购买的数量比第一次多20千克，以每千克9元售出100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价50%售完剩余的水果．
（1）求第一次水果的进价是每千克多少元？
（2）该果品店在这两次销售中，总体上是盈利还是亏损？盈利或亏损了多少元？