华中师大一附中理科实验班举行投篮比赛，下表显示了比赛的结果，上行的值表示投篮中的个数，下行的值表示投中 个球的参赛人数.
对比赛的结果还知道如下情况：
（1）获胜者投中 个球；
（2）对投中 个球或 个以上球的参赛者来说，每人平均投中 个球；
（3）对投中 个球或 个以下球的所有参赛者来说，每人平均投中 个球；
问本次比赛所有参赛者投中的球的总数是多少?
如图,已知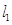
∥
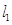,点A, D在上,点B, C在上,试说明△EGO与△FHO面积相等｡
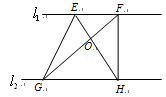
问题情境：如图①，在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；
特例探究：如图②，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB="AC," CF⊥AE于点F,BD⊥AE于点D.证明：△ABD≌△CAF;
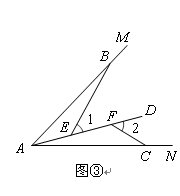
归纳证明：如图③，点BC在∠MAN的边AM、AN上，点EF在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB="AC," ∠1=∠2=∠BAC.求证：△ABE≌△CAF;
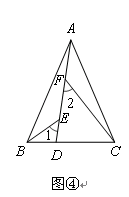
拓展应用：如图④，在△ABC中，AB=AC，AB＞BC.点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC.若△ABC的面积为15，则△ACF与△BDE的面积之和为.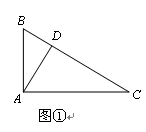
如图，A、B、C三点在同一直线上，分别以AB、BC为边，在直线AC的同侧作等边△ABD和等边△BCE，连接AE交BD于点M，连接CD交BE于点N，连接MN得△BMN，试判断△BMN的形状，并说明理由.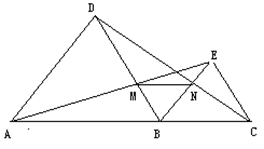
已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF．(8分)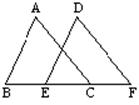 
如图，在8×6正方形方格中，点A、B、C在小正方形的顶点上.
（1）在图中画出与△ABC关于直线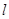
成轴对称的△A
；
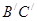（2）线段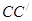
被直线；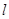
（3）在直线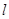上找一点P，使PB+PC的长最短，不写作法，保留作图痕迹.