问题情境：如图①，在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；
特例探究：如图②，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB="AC," CF⊥AE于点F,BD⊥AE于点D.证明：△ABD≌△CAF;
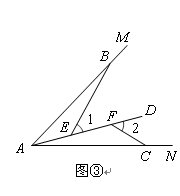
归纳证明：如图③，点BC在∠MAN的边AM、AN上，点EF在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB="AC," ∠1=∠2=∠BAC.求证：△ABE≌△CAF;
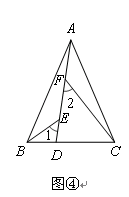
拓展应用：如图④，在△ABC中，AB=AC，AB＞BC.点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC.若△ABC的面积为15，则△ACF与△BDE的面积之和为 .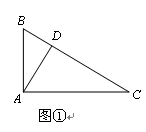
已知，如图所示，在Rt△ABC中，∠C＝90°，有一内接正方形DEFC，连接AF交DE于G，AC＝15，BC＝10，求EG的长．
如图，甲袋内共有4张牌，牌面分别标记数字1，2，3，4；乙袋内共有3张牌，牌面分别标记数字2，3，4．甲袋中每张牌被取出的机会相等，且乙袋中每张牌被取出的机会也相等．分别从甲乙两袋中各随机抽取一张牌，请用列表或画树形图的方法，求抽出的两张牌面上的数字之和大于5的概率．
小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（B，F，D在同一条直线上）．一直小敏的眼睛与地面距离为1．5m，求这栋建筑物CD的高度（参考数据：
，结果保留整数）
如图，图中的小方格都是边长为1的正方形，△ABC的A、B、C三点坐标为A（2，0）、B（2，2）、C（6，3）．
（1）请在图中画出一个△
，使△与△ABC是以坐标原点为位似中心，相似比为2的位似图形．
（2）求△的面积．
解方程：