在直角坐标系中，有以 为顶点的正方形，设它在折线 上侧部分的面积为 ，求 关于 的函数关系式.
（本题8分）已知直线y＝2x－b经过点（1，－1），求关于x的不等式2x－b≥0的解集．
如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如
， 
，
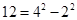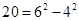，因此4，12，20都是“神秘数”
（1）28和2012这两个数是“神秘数”吗？为什么？
（2）设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？
（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？
如图：某校一块长为2a米的正方形空地是七年级四个班的清洁区，其中分给七年级（1）班的清洁区是一块边长为（a－2b）米的正方形，（0<b<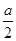
），
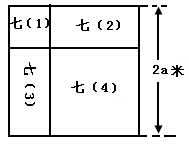
（1）分别求出七（2）、七（3）班的清洁区的面积；
（2）七（4）班的清洁区的面积比七（1）班的清洁区的面积多多少平方米？
已知a+b=4，ab=－2，求a2－ab+b2的值．
已知10a=5，10b=6，求:
（1）
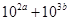的值；
（2）
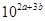的值