(1)已知平面内有 条直线 和 .直线 和 相交于一点,直线 和 也相交于一点,试确定这 条直线共有多少个交点?并说明你的理由.
(2)作第 条直线 与(1)中的直线 平行,说明以这 条直线的交点为端点的线段有多少条?
如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为米.
如图,将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6cm(如箭头所示),则木桩上升了()
| A.6sin15°cm | B.6cos15°cm | C.6tan15° cm | D.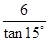 cm cm |
如图,△OAB是边长为2的等边三角形,过点A的直线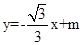 与x轴交于点E .
与x轴交于点E . 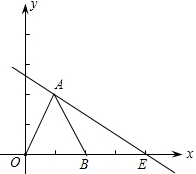
(1)求点E的坐标;
(2)求过 A、O、E三点的抛物线解析式;
(3)若点P是(2)中求出的抛物线AE段上一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.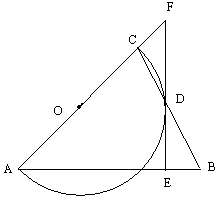
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,BE=1,求cosA的值.
如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y= 的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
 (1)求一次函数与反比例的解析式;
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣ >0的解集.
>0的解集.