已知 ,求 的值.
若单项式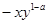 与
与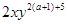 是同类项,当
是同类项,当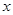 、
、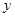 满足
满足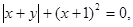 时,求代数式
时,求代数式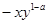
 的值.
的值.
解方程:
(1)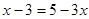 ;
;
(2)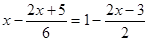
有理数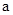 ,
,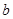 ,
, 在数轴上的位置如图所示,试化简下式:
在数轴上的位置如图所示,试化简下式: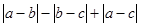
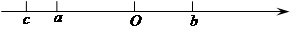
把下列各数填入相应的数集合中: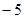 ,
,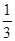 ,
, ,0,
,0,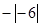 ,
,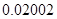 ,
,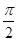
正数{…};
整数{…};
无理数{…}。
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4(第一步)
= y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
| A.提取公因式 |
| B.平方差公式 |
| C.两数和的完全平方公式 |
| D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.