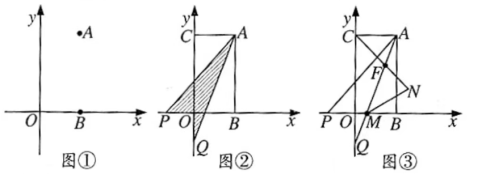
已知在平面直角坐标系中点 ,点 ,且满足 .
(1)求点 ,点 的坐标;
(2)已知点 ,点 从 点出发,沿 轴负方向以 个单位每秒的速度移动.同时点 从 点出发,沿 轴负方向以 个单位每秒的速度移动,某一时刻,如图②所示,且 .求点 移动的时间?
(3)在(2)的条件下, 交 轴于 ,作 的角平分线交于点 ,如图③所示,判断 是否为定值,若是定值求其值;若不是定值,请说明理由.
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.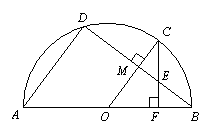
(1)求⊙O的半径;
(2)求证:CE=BE.
已知:如图,在△ABC中,AB="AC=" 5,BC= 8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
已知关于x的一元二次方程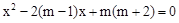 .
.
(1)若此方程有实数根,求m的取值范围;
(2)若x=-1是这个方程的一个根,求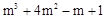 的值.
的值.
已知a,b为实数,且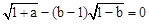 ,求
,求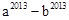 的值.
的值.
如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为160cm2,那么纸板各角应切去边长为多大的正方形?