某校九年级(1)班 名学生参加 跳绳体育考试. 跳绳次数与频数经统计后绘制出下面的频数分布表( 表示为大于等于 并且小于 )和扇形统计图,(如图).


(1)求 的值;
(2)求该班 跳绳成绩在 分以上(含 分)的人数占全班人数的百分比;
(3)根据频数分布表估计该班学生 跳绳的平均分大约是多少?并说明理由.
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB.OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.求A、B、C三点的坐标;
求此抛物线的表达式
连接AC、BC,若点E是线段AB上的一个动点(与点A.点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由
如图是一种新型滑梯的示意图,其中线段PA是高度为6米的平台,滑道AB是函数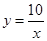 的图象的一部分,滑道BCD是二次函数图象的一部分,两滑道的连接点B为抛物线的顶点,且点B到地面的距离为2米,当甲同学滑到点C时,距地面的距离为1米,距点B的水平距离CE也为1米.
的图象的一部分,滑道BCD是二次函数图象的一部分,两滑道的连接点B为抛物线的顶点,且点B到地面的距离为2米,当甲同学滑到点C时,距地面的距离为1米,距点B的水平距离CE也为1米.
试求滑道BCD所在抛物线的解析式;
试求甲同学从点A滑到地面上点D时,所经过的水平距离.
如图,AB是⊙O的直径,点P是⊙O上的动点(P与A,B不重合),连结AP,PB,过点O分别作OE⊥AP于E,OF⊥BP于F.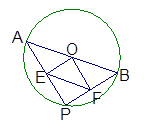
若AB=12,当点P在⊙O上运动时,线段EF的长会不会改变.若会改变,请说明理由;若不会改变,请求出EF的长
若AP=BP,求证四边形OEPF是正方形
在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?

若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径?
能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
如图,小明晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,从C处继续往前走2米到达E处时,测得影子EF的长为2米,B、C、D、E、F在同一条直线上,已知小明的身高是1.6米,求路灯A的高度?